Parameters in Photogrammetric Software for Small-Format Oblique Camera System on Unmanned Aerial Vehicle

Bannakulpiphat, T.¹ and Santitamnont, P.^1,2,*

¹Department of Survey Engineering, Chulalongkorn University, Bangkok 10330, Thailand

²Center of Excellence in Infrastructure Management, Chulalongkorn University, Bangkok, Thailand

*Corresponding Author

Abstract

Utilizing small-format oblique camera systems to capture simultaneous nadir and oblique photographs from unmanned aerial vehicles (UAVs) is a common practice in modern photogrammetry. Oblique photographs provide enhanced geometric insights into building side views, terrain morphology, and vegetation, thereby enriching interpretation and classification. However, the design of camera rig parameters and their precise mathematical modeling for small-format oblique camera systems in multi-view processing is essential to ensure accurate representation of the physical camera geometry and results. This study investigates the camera rig parameters of the ‘3DM-V3' small-format oblique camera system, focusing specifically on the relative relationship between nadir and oblique cameras, within two prominent photogrammetric software: PIX4Dmapper and Agisoft Metashape. The research concludes that optimal parameterization involves fully constrained relative translation parameters (T_X, T_Y, T_Z) _rel for the four oblique cameras, while setting approximate initial estimates as free constrained for relative rotation parameters (R_X, R_Y, R_Z)_rel. This approach aligns with the physical geometry of the camera system and yields a precise camera model, as confirmed through bundle block adjustment (BBA) computations. PIX4Dmapper yields horizontal and vertical root mean square errors (RMSE) of 0.023 m and 0.019 m, respectively, while Agisoft Metashape results in RMSE of 0.018 m and 0.046 m. These RMSE values, considering the ground sample distance and ground control point accuracy, reflect the robustness of the approach. The insights from this research offer valuable guidance for industries, facilitating informed decisions regarding the selection of appropriate software and parameters for small-format oblique camera systems mounted on UAVs, thus ensuring consistency between theoretical models and real-world applications.

Keywords: Camera Model, Camera Rig, Oblique Camera, Oblique Photograph, UAV, Small-format Oblique Camera Systems

1. Introduction

Multi-head camera systems are widely used in modern photogrammetry for capturing simultaneous nadir and oblique photographs from unmanned aerial vehicles (UAVs) [1][2] and[3]. These systems provide oblique photographs rich in geometric details, such as side views of buildings and the vegetation canopy on the terrain. Such details significantly enhance interpretation and classification compared to traditional nadir photographs [4] and [5]. Multi-head camera systems improve the information available for mapping and increase the efficiency of mapping missions. They facilitate the acquisition of multi-view photographs, leading to an extensive dataset for subsequent multi-view geometry and point-cloud processing. This enhancement is crucial for improved keypoint generation, which plays a vital role in automated processing using photogrammetric computer vision software [6] and [7].

Historically, unmanned aerial vehicles (UAVs) were primarily developed and used by the military for surveillance, reconnaissance, and other tactical purposes [8] and [9]. Recently, however, UAVs have been extensively adopted for civilian and commercial applications, ranging from package delivery and agriculture to mapping and engineering inspection.

Many of these applications necessitate the creation of 3D maps and point clouds, which serve to reference the geographic location of terrain and aid in design [10] and [11]. Photogrammetric mapping software heavily relies on aerial photographs taken by a single camera installed on a UAV. However, the accuracy of the resulting maps and models is influenced by various factors, including the instrument used, mission planning and execution methods, and software for image processing [12]. Addressing these challenges, a notable development in the industry is the emergence of manufacturers producing small-format oblique camera systems. Designed for integration with off-the-shelf UAVs for mapping and inspection purposes, these systems have garnered interest due to their affordability and ease of operation. While UAVs equipped with these cameras still operate under national air traffic control, they offer a safer alternative and significantly more cost-effective compared to manned aircraft equipped with large-format oblique camera systems.

Researchers have explored the use of oblique camera systems with multiple cameras due to the advantageous image orientation these systems offer. Specifically, multi-camera systems possess superior ray intersection geometry compared to nadir-only image blocks. However, these systems face challenges stemming from factors such as varying scale, occlusion, and atmospheric influences, which are difficult to model and can complicate image matching and bundle adjustment tasks. For instance, Gerke et al., [13] delved into the processing of oblique airborne image sets, focusing on tie point matching across different viewing directions, bundle block adjustment accuracy, the influence of overlap on accuracy, and the distribution of control points and their impact on point accuracy. Karel et al., [14] introduced a method to significantly reduce the number of tie points, and consequently the unknowns, before the bundle block adjustment, ensuring the preservation of orientation and quality calibration for aerial blocks from multi-camera platforms. Alsaidik et al., [15] showcased a hybrid acquisition system tailored for UAV platforms, merging multi-view cameras with LiDAR scanners to enhance data collection. Their research underscores the synergies between LiDAR and photogrammetry, emphasizing their combined potential to enhance data quality. They also highlight the importance of these hybrid systems in efficiently generating 3D geospatial information. While such systems can significantly increase multi-view mapping information and image overlap, it is crucial to account for the oblique effect introduced by angled cameras to the structure of the camera system, particularly in terms of the angles and distances of the cameras in a multi-head, small-format oblique camera system. The objective of this research is to examine the parameters of the camera rig and their numerical modeling in the “3DM-V3” small-format oblique camera systems. The aim is to understand the impact of different photogrammetric software packages on processing aerial photographs, especially the relative relationship between the nadir camera and oblique cameras within these systems. To accomplish this, mathematical models were created and compared using two commonly used photogrammetric software packages: PIX4Dmapper (version 4.7.5) and Agisoft Metashape (version 1.8.3). Both are globally recognized in the photogrammetric computer vision field and provide settings for the parameters and weighting of the camera rig. Highlighting discrepancies in results based on the software packages broadens understanding about UAVs equipped with oblique camera systems and the application of Structure-from-Motion (SfM) technologies. In this study, the same aerial photographs used in a prior study by Bannakulpiphat et al., [16] were processed. The conclusions from their research underlined the significance of optimizing camera rig parameters for UAV-mounted small-format oblique camera systems to ensure alignment with actual rig geometries. This paper examines the variations in camera rig parameters across the photogrammetric software and compares these parameters with the real-world dimensions of the oblique camera systems, ensuring consistent camera geometry. Furthermore, the multi-view geometry techniques offered by both software packages are used to compare the supplementary coordinates derived from 3D measurements.

2.Materials and Methods

2.1 Data Acquisition

The study area for this research was the geodetic GNSS and UAV testing field at the Center of Learning Network for Region (CLNR), supervised by the Faculty of Engineering, Department of Surveying Engineering. This field is located in the province of Saraburi, central Thailand (Latitude: 14.523676°N, Longitude: 101.023542°E) covering an area of approximately 0.8 km². A map of the area is shown in Figure 1(a). The aerial photographs used for this research were captured using a vertical take-off and landing (VTOL) aerial vehicle, named Loong 2160 VTOL, as depicted in Figure 1(b). This VTOL was equipped with a "FOXTECH 3DM-V3" small-format oblique camera system, designed specifically for mapping and surveying purposes, and is shown in Figure 1(c).

Figure 1: (a) Distribution of the GCPs (yellow triangles); (b) Loong 2106 VTOL used for the study; and (c) the FOXTECH 3DM-V3 camera

Table 1: UAV and camera specifications

The camera system consists of one nadir camera and four 45-degree oblique cameras, each enclosed in a rig with its own SD card slot for separate storage. The technical specifications of the UAV and camera used in this study are summarized in Table 1.

The flight mission was conducted in a single-strip block format, typical of conventional photogrammetric mapping. The flight route, managed by ARDUPILOT software, maintained an average altitude of 150 meters above ground level, with an overlap of 80% and a side lap of 60%. The mission comprised 12 flight lines and captured a total of 2,995 photographs, averaging 599 photographs per camera. Ground control points (GCPs) were measured on the same day using the real-time kinematics (RTK) GNSS technique, achieving a horizontal accuracy of 2 cm and a vertical accuracy of 5 cm. A total of 14 GCPs were distributed across the study area (see Figure 1a) and used to georeference the photogrammetric block.

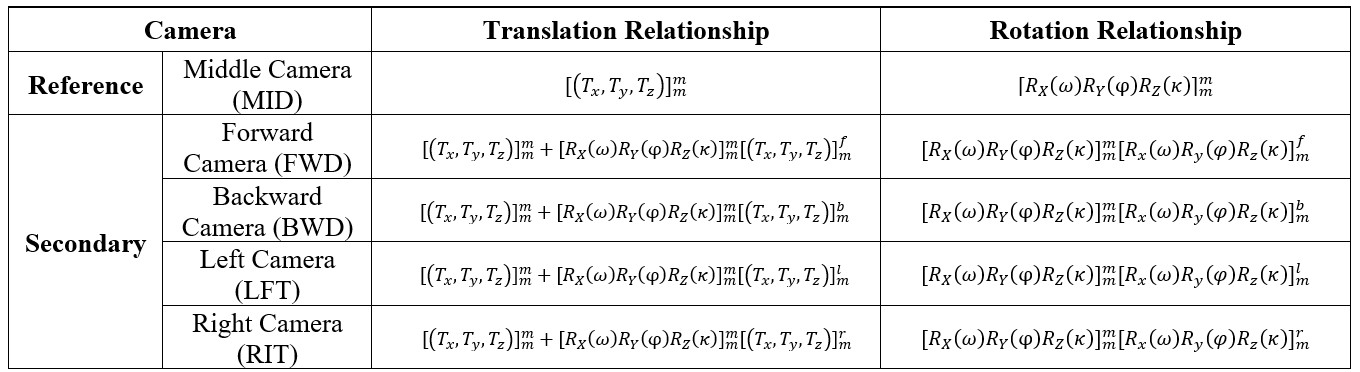
2.2 Mathematical Modeling of the Small-Format Oblique Camera Systems

Small-format oblique camera systems consist of multiple cameras mounted on a camera-rig structure, necessitating a mathematical model that effectively links these different cameras.

To develop an accurate camera rig model, understanding the precise relationship between each secondary camera and the reference camera on the camera rig is essential. This relationship is defined by the relative translation and rotation parameters, which describe the exact geometric characteristics of the cameras' interrelationship. These rig parameters are crucial for subsequent bundle block adjustment (BBA), wherein the orientation parameters of these cameras are optimized simultaneously to create a 3D model of the object or area of interest. Thus, the mathematical modeling of a small-format oblique camera system involves the following geometric relationship characteristics:

1. A single camera in a small-format oblique camera system is typically designated as the reference camera and has a known position (T_m) and orientation (R_m) in the world coordinate system.
2. The other cameras are secondary cameras, each with its own position (T_s) and orientation (R_s) in the same world coordinate system.
3. Each secondary camera is defined relative to the reference camera by known relative translation (T_rel) and rotation (R_rel).

The exterior orientation parameters of every camera in the multi-head camera system, except for the reference camera, are computed using specific equations. The reference camera serves as the benchmark for calculating the positions and orientations of the secondary cameras, as detailed in Equations (1) and (2):

T_s =T_m + R_mT_rel

Equation 1

R_s = R_mRrel

Equation 2

The positions of a three-dimensional point (X') in the camera coordinate systems of the reference and the secondary camera can be given by Equation (3) and Equation (4), respectively.

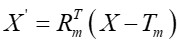
Equation 3

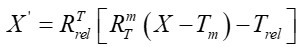
Equation 4

Where T represents the position of the camera projection center in the world coordinate system, represents the rotation matrix that defines the camera orientation, X represents a 3D point in the world coordinate system, and X' represents a 3D point in the camera coordinate system [17]. Understanding these geometric relationships is fundamental for bundle block adjustment (BBA), where the orientation parameters of the cameras are optimized simultaneously to generate a 3D model of the target object or area. This mathematical modeling of the small-format oblique camera system provides essential insights into the precise geometric characteristics governing the relationships between different cameras on the rig. As a result, it enables more advanced tasks like 3D modeling and aerial mapping to produce results consistent with the real world. Therefore, the relative translation (T_rel) and rotation (R_rel) parameters are crucial in defining the modeling of the small-format oblique camera system, ensuring both precision and real-world geometric consistency. The small-format oblique camera systems utilized in this research are illustrated in Figure 2 and further detailed upon in Table 2 and Table 3.

2.3 Photogrammetric Processing

The goal of photogrammetric processing in this study was to establish a mathematical model for the rig parameters of a small-format oblique camera system. The results were evaluated in terms of geometry and uncertainty using two commercial UAV processing software applications, namely PIX4Dmapper and Agisoft Metashape. These applications use photogrammetric computer vision techniques to align photographs through structure-from-motion, constrain block datum with ground control points (GCPs), and simultaneously solve the bundle block adjustment (BBA) with camera self-calibration by assigning proper weight to these observations. The software calculates the relationship between the photographic coordinates and the camera model, linking them to the coordinates of the GCPs.

Additionally, the software can process aerial photographs and calculate the relationship of the camera rig parameters, based on the relative positions between the reference camera and the secondary cameras. When processing nadir and oblique photographs, additional settings account for the camera rig parameters to bridge the cameras. The camera rig parameters, crucial for linking small-format oblique camera systems in this study, facilitate the measurement of relative displacements among cameras and their individual physical characteristics.

Figure 2: Exterior orientation parameters and the mathematical model of small-format oblique camera systems

Table 2: Symbols for each camera parameter matrix in the small-format oblique camera systems

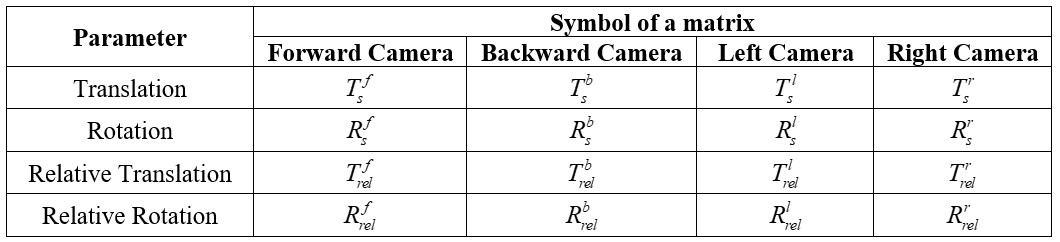
Table 3: Mathematical relationships between the reference camera and the secondary camera in the small-format oblique camera systems

However, the rotation parameters remain ambiguous, as the manufacturer did not supply model values for the proprietary camera system. Consequently, an initial approximate value is used, allowing the software to fine-tune the outcome through a numerical method. In modeling the small-format oblique camera system, both PIX4Dmapper and Agisoft Metashape provide features to process aerial photography blocks that incorporate multiple cameras. Each program allows for setting parameters for every camera in the oblique camera system, such as relative translation and relative rotation, along with weights for camera-rig constraints. After processing, the program optimizes these parameters based on numerical computation. In addition to the relative translation and rotation parameters obtained from the data processing software, the software can also autonomously handle the interior orientation parameters of each camera in small-format oblique camera system.

This means that within the data processing software, parameters can be set, and the software employs a numerical method to deduce optimal values. These include the focal length (f), the principal point (c_x, c_y),the radial lens distortion coefficients (R1, R2, R3), and the tangential lens distortion coefficients (T1, T2). This comprehensive process is commonly referred to as in-situ calibration.

3. Results and Discussions

3.1 Parameterization and Numerical Modeling of Small-Format Oblique Camera Systems

The research begins by processing aerial photographs from small-format oblique camera systems with these systems being freely constrained by both relative translation and rotation parameters during numeric processing. However, the results of image processing revealed inconsistencies between the exterior orientation parameters of the oblique systems and the physical geometry of the camera systems. To address this, it is necessary to determine the camera rig parameters and perform numerical modeling for small-format oblique camera systems, ensuring consistency with the physical geometry of the camera systems and allowing for the setting of weight in terms of precision. Table 4 shows the constraints of the weight for the camera rig parameters used in this research.

For the relative translation parameters, denoted as (T_x, T_y, T_z)_relⁿ, where n ranges from 1 to 4, all four sets of offset values for the oblique cameras are defined as “fully constrained”. This is physically consistent with the actual distance measurement from the reference camera to the secondary camera. The relative rotation parameters, denoted as (R_x, R_y, R_z)_relⁿ , where n ranges from 1 to 4, for each reference camera and oblique cameras, are approximated as initial estimates and set as "free constrained" during numerical processing. The final camera model, resulting from the bundle block adjustment computation, confirms the precise geometry and reveals consistent rig parameters as expected. The results of the final numerical modeling are depicted in Table 5 for PIX4Dmapper and in Table 6 for Agisoft Metashape. Furthermore, Figure 3 shows the resulting rotations (R_x, R_y, R_z) in a bar graph, compared to the mean values of the four oblique cameras.

3.2 Quality Control for Bundle Block Adjustment Result

To ensure the precision of the photogrammetric results, an in-depth examination of ground control points (GCPs) was undertaken before the aerial triangulation process; this utilized a total of 14 GCPs. For anomaly detection, the GCPs were divided into two groups: Group 1, which included 7 partial GCPs, and Group 2, which contained 7 partial checkpoints (CPs). The root mean square error (RMSE) values for the two groups were analyzed along each axis, and no abnormal values were detected (refer to Table 7 and Figure 4). Based on these findings, the final aerial triangulation of the five-camera block was executed, incorporating all 14 GCPs. The outcomes of this assessment, detailed in Table 8, are integral to ensuring the accuracy and reliability of the photogrammetric output.

3.3 Comparison of the Consistency of 3D Measurement from Two Photogrammetric Software

After defining the physical geometry of the mathematical model for the small-format oblique camera system, this study utilized the multi-view stereo techniques offered by both software programs to compare the coordinates obtained from 3D measurements of 30 sample points in an open field, as illustrated in Figure 5. These sample points were strategically selected along roads or adjacent to buildings, chosen for the ease of surveying in these locations and their relevance to future design projects and related tasks. The RMSE results revealed differences of 0.065 m in the horizontal component and 0.110 m in the vertical component between the two software packages. While these differences exist, they are not significant. Potential explanations for these nominal error values include the state-of-the-art algorithms and error correction methodologies used in both software packages. Additionally, external factors such as temporal changes affecting light conditions, minor camera misalignments, and systemic errors from GPS or GNSS—such as atmospheric delays or multipath effects-might also contribute to these variances.

Table 4: Proposed weights for camera-rig parameters constraints

Table 5: Solutions for the relative translation and rotation parameters in the case of PIX4Dmapper

Table 6: Solutions for the relative translation and rotation parameters in the case of Agisoft Metashape

Table 7: RMSE values for anomaly detection in GCPs based on the nadir photographs block

Table 8: RMSE values for the combined five-camera block, based on the full GCPs

Figure 3: Comparison of deviations from forty-five degrees for each oblique camera by two software packages. Dashed lines indicate average angles: red for PIX4Dmapper and green for Agisoft Metashape

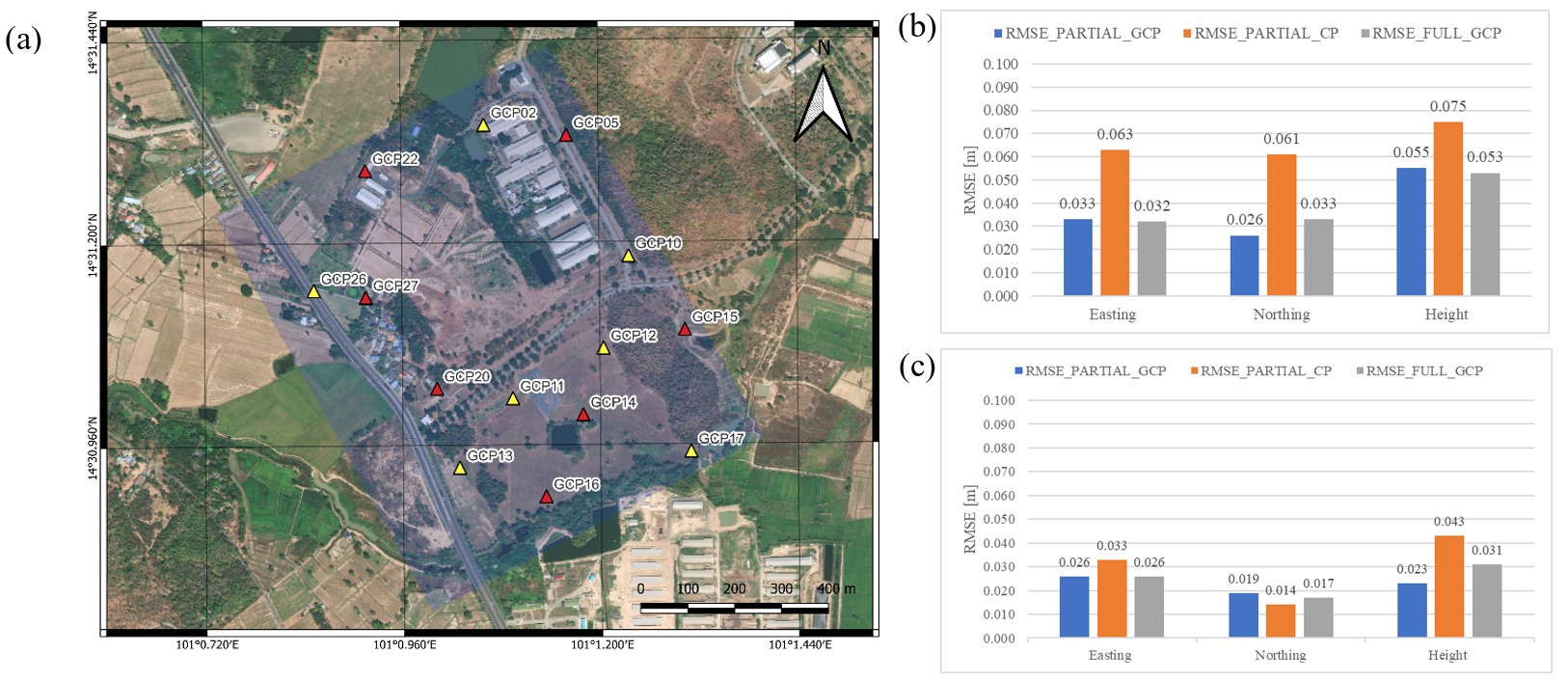
Figure 4: (a) Distribution of points for anomaly investigation, with partial GCPs represented as yellow triangles and partial CPs as red triangles. (b) and (c) display RMSE value comparisons for PIX4Dmapper and Agisoft Metashape, respectively

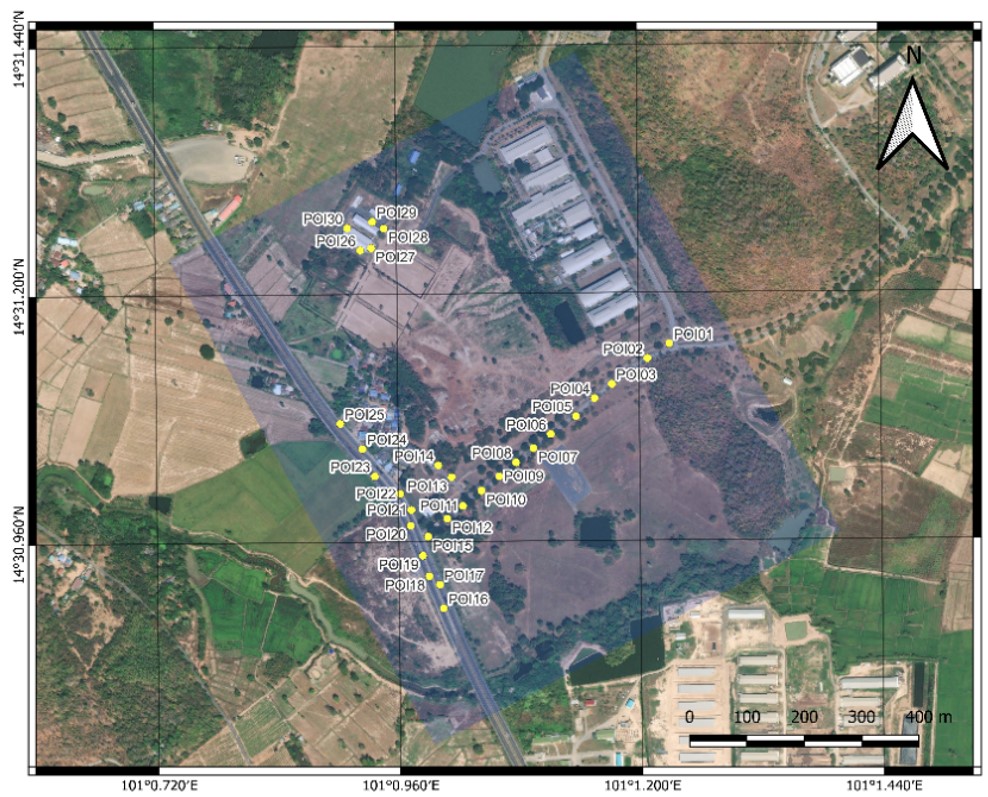
Figure 5: Distribution of the 30 sample points (yellow circles) in the open field of the study area (blue area)